7.2.3 平行线的性质
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行. 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?这就是下面要学习的平行线的性质.
类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角的关系.
探究
如图7.2-9,画两条平行线a∥b,然后任意画一条截线c与这两条平行线相交,度量所形成的八个角的度数.
在∠1,∠2,…,∠8中,哪些是同位角?它们的度数有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系.
利用信息技术工具改变截线c的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗?
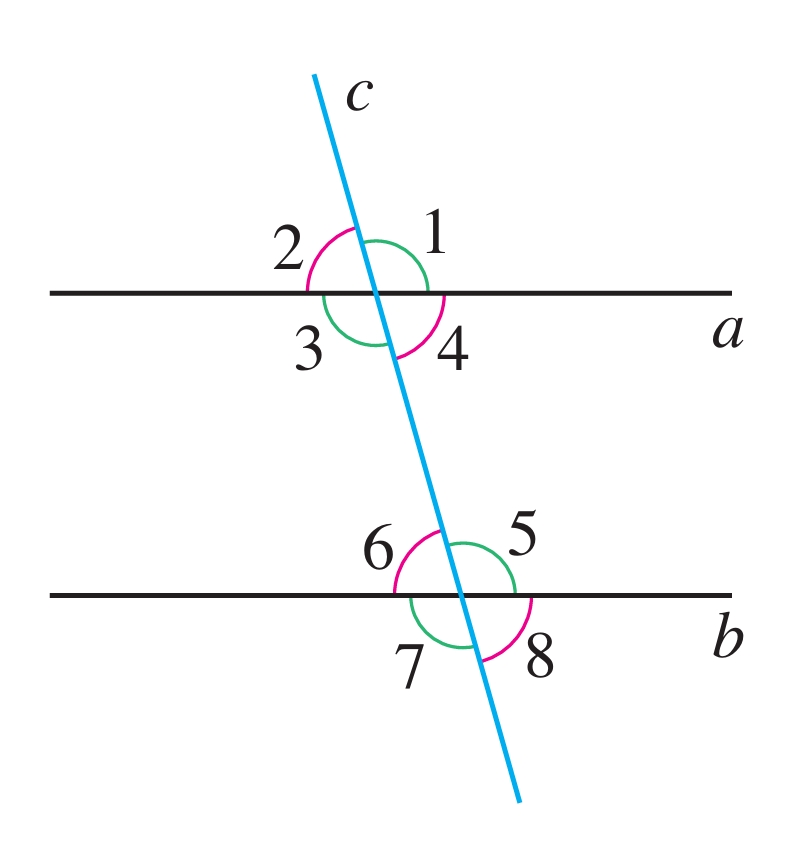
图7.2-9
一般地,平行线具有性质:
性质1 两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
前面我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗?
如图7.2-10,直线a∥b,c是截线. 根据“两直线平行,同位角相等”,可得∠1=∠2. 而∠3和∠2互为对顶角,所以∠3=∠2. 所以∠3=∠1. 这样就得到了平行线的另一个性质:
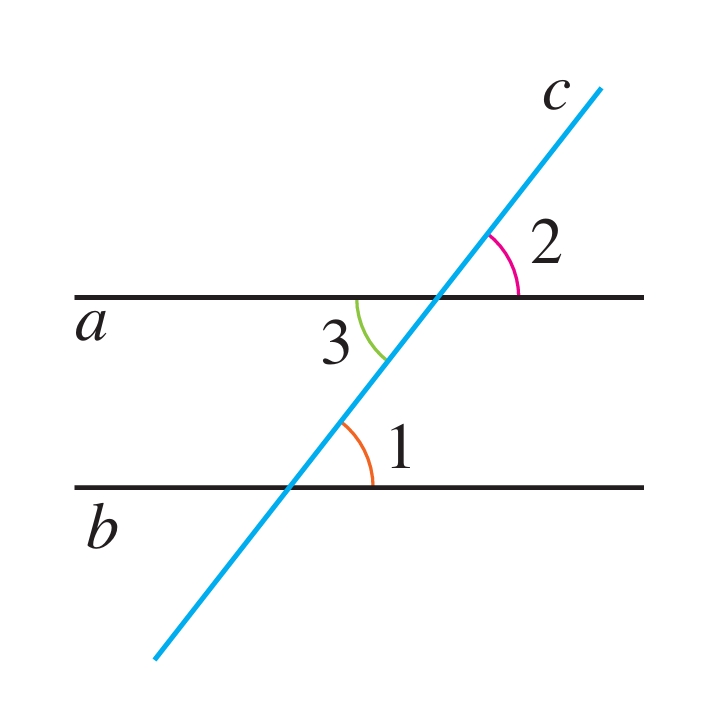
图7.2-10
性质2 两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
类似地,由性质1或性质2,可以推出平行线关于同旁内角的性质(请你自己完成推理过程):
性质3 两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
例2
图7.2-11是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D,∠C分别是多少度?
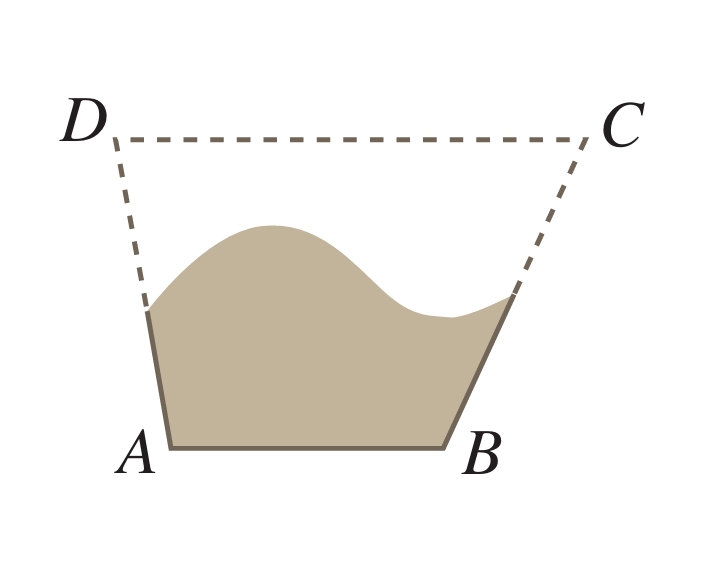
图7.2-11
解:
因为梯形上、下两底DC与AB互相平行,根据“两直线平行,同旁内角互补”,可得∠A与∠D互补,∠B与∠C互补. 于是
∠D=180°-∠A=180°-100°=80°,
∠C=180°-∠B=180°-115°=65°.
所以梯形的另外两个角∠D,∠C分别是80°,65°.
练习
-
如图,直线a∥b,∠1=54°,∠2,∠3,∠4各是多少度?
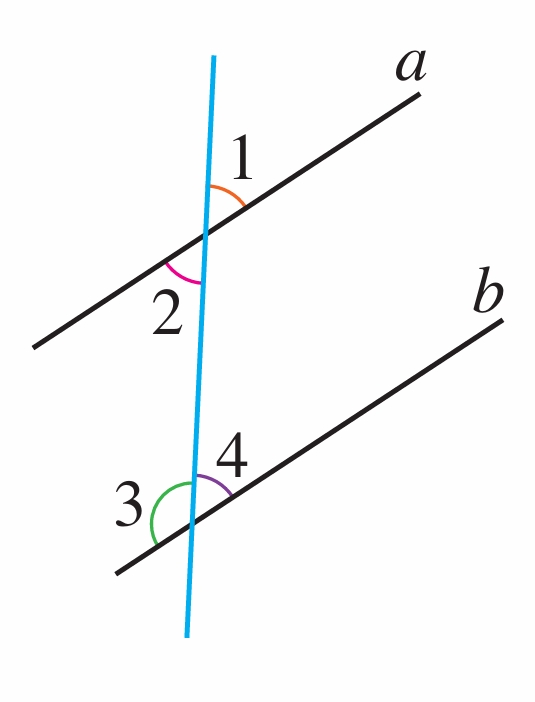
(第1题)
-
如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
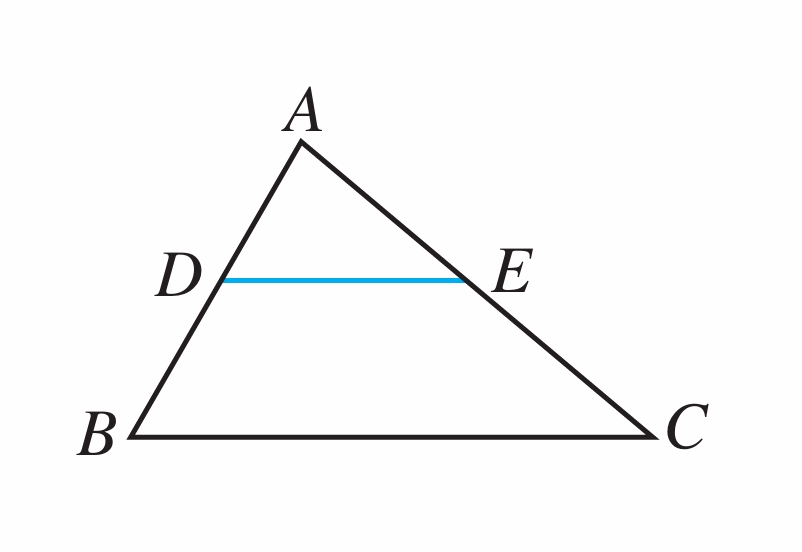
(第2题)
-
将一个直角三角尺与两边平行的纸条如图放置,则下列结论正确的是________(填序号).
① ∠1=∠2; ② ∠4+∠5=180°; ③ ∠1+∠4=90°; ④ ∠4+90°=∠3.
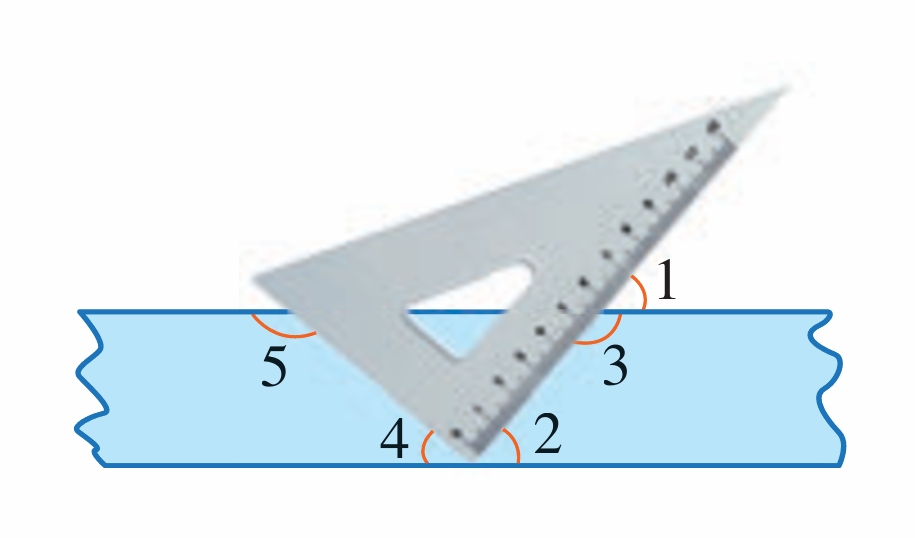
(第3题)
前面我们学习了平行线的判定和性质,在解决问题时,经常需要把它们结合起来使用.
例3
如图7.2-12,已知直线a∥b,∠1=∠3,那么直线c与d平行吗?为什么?
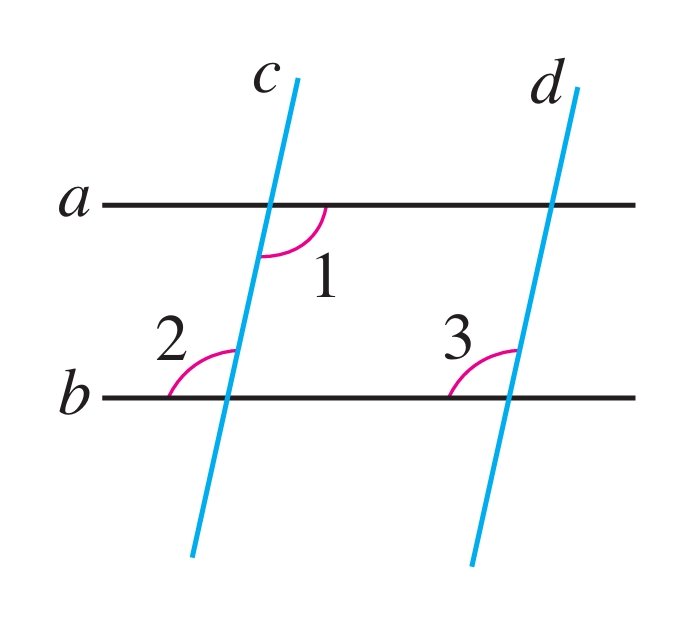
图7.2-12
分析:
由于∠2和∠3是直线c与d被直线b所截形成的同位角,所以如果能推出∠2=∠3,就可以判断直线c与d平行. 而已知∠1=∠3,所以只需由直线a∥b,推出∠1=∠2.
解:
直线c与d平行. 理由如下:
如图7.2-12,
∵ a∥b,
∴ ∠1=∠2(两直线平行,内错角相等).
又 ∠1=∠3,
∴ ∠2=∠3.
∴ c∥d(同位角相等,两直线平行).
你能用其他方法判定直线c与d平行吗?
例4
如图7.2-13,∠1=∠2,∠3=50°,∠ABC等于多少度?
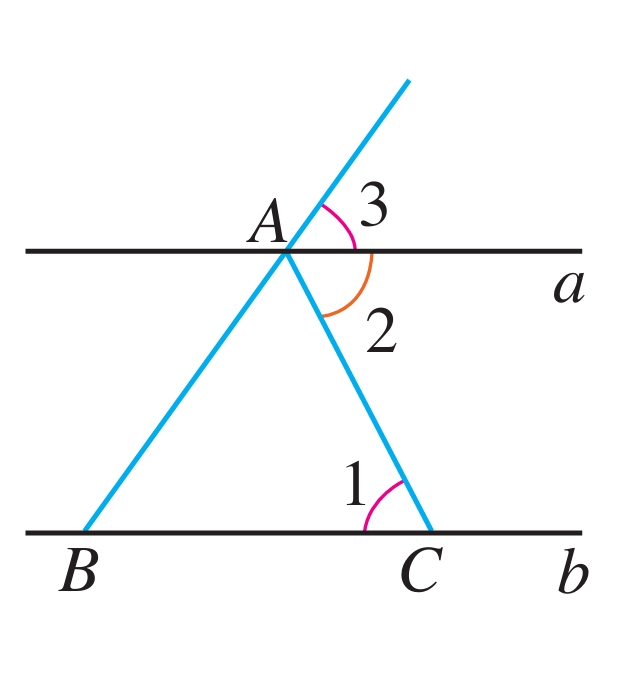
图7.2-13
分析:
由于∠3的大小是已知的,所以可以尝试推导∠ABC与∠3的大小关系. 而由已知条件∠1=∠2,可以推出a∥b,从而可以得到∠ABC=∠3.
解:
∵ ∠1=∠2,
∴ a∥b(内错角相等,两直线平行).
∴ ∠3=∠ABC(两直线平行,同位角相等).
又 ∠3=50°,
∴ ∠ABC=50°.
练习
-
如图,如果直线a∥b,∠1+∠2=180°,那么直线b和c平行吗?为什么?
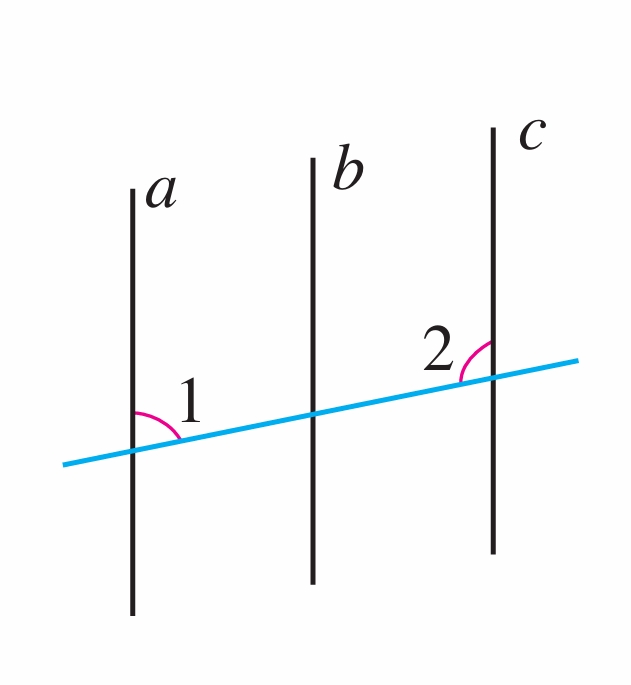
(第1题)
-
如图,AB∥CD,且∠1=∠2,那么直线BE与CF平行吗?为什么?
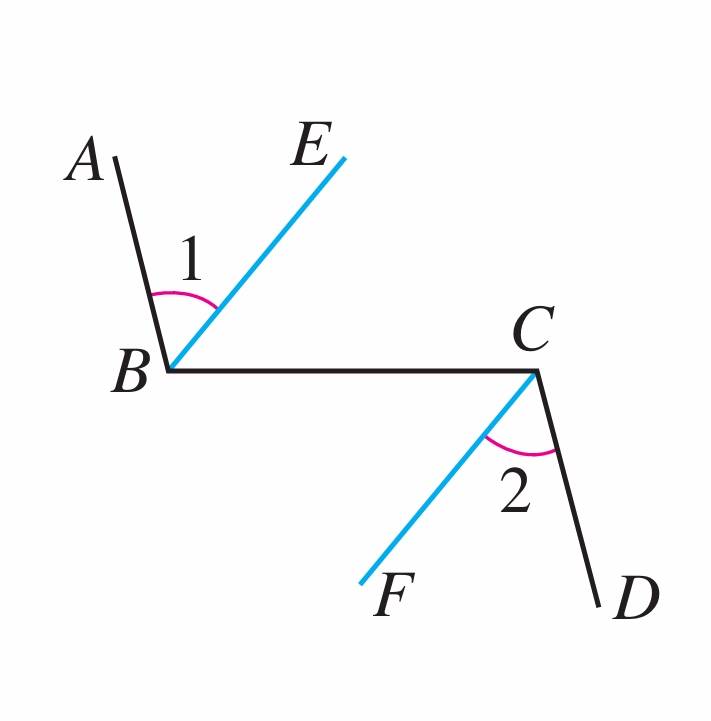
(第2题)
本节小结
- 平行线的性质1:两直线平行,同位角相等
- 平行线的性质2:两直线平行,内错角相等
- 平行线的性质3:两直线平行,同旁内角互补
- 平行线的性质与判定的区别:判定是由角的关系推出直线平行,性质是由直线平行推出角的关系
- 在解决问题时,经常需要将平行线的性质与判定结合起来使用