7.2.2 平行线的判定
我们已经知道,如果平面内的两条直线不相交,就可以判断这两条直线平行. 但是,由于直线是无限延伸的,检验它们是否相交有困难,所以难以直接根据两条直线不相交来判断它们是否平行. 那么,有没有其他判定方法呢?
思考
在如图7.2-3利用直尺和三角尺画平行线的过程中,三角尺起着什么样的作用?
记图7.2-3中紧贴三角尺的直尺的边所在直线为c,得到图7.2-6,可以看出,画互相平行的直线a和b,实际上就是分别画相等的∠1和∠2的一条边,而∠1和∠2正是直线a,b被直线c截得的同位角. 这说明,如果同位角∠1=∠2,那么a∥b.
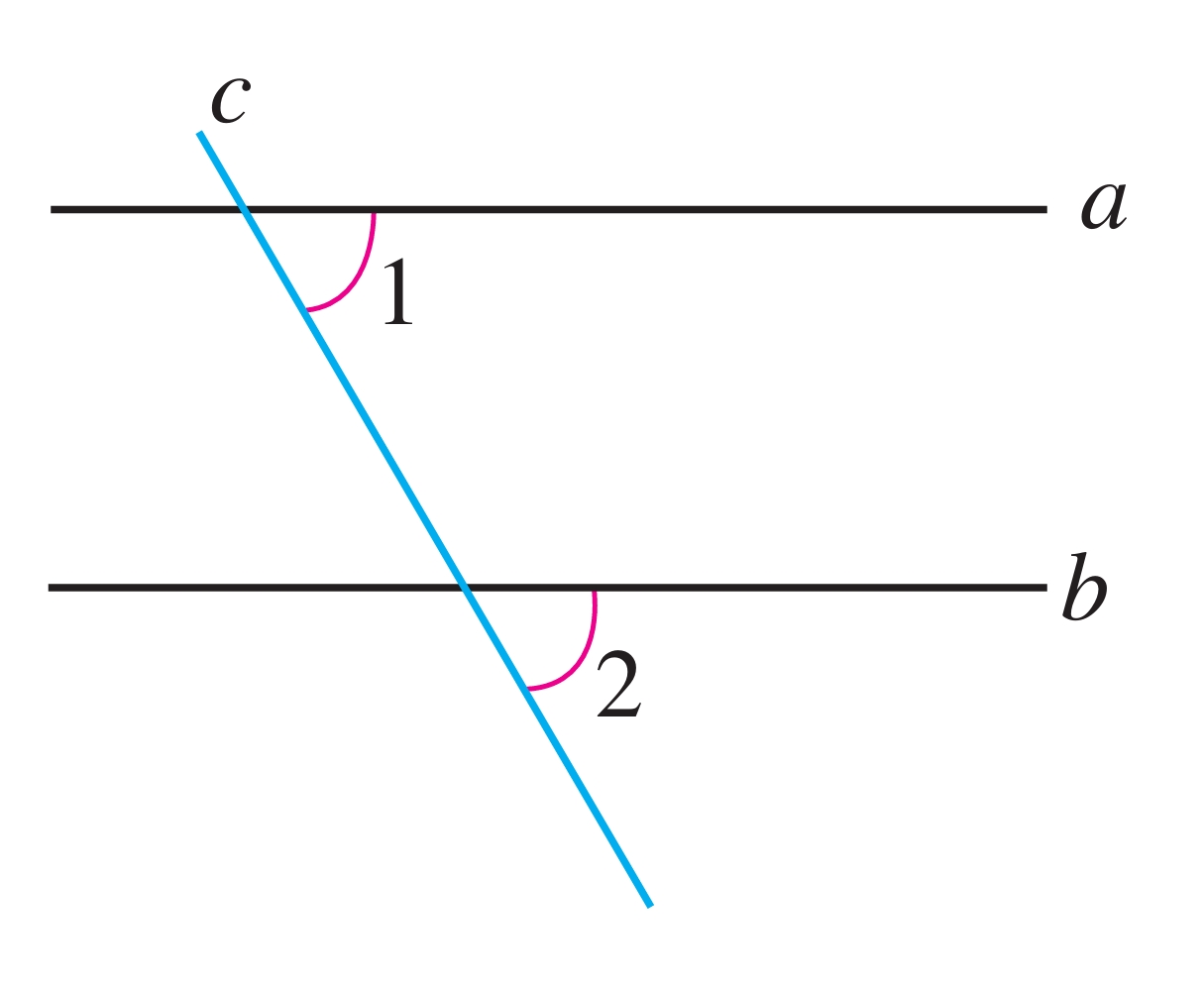
图7.2-6
一般地,有如下利用同位角判定两条直线平行的基本事实:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角. 由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
探究
如图7.2-7,直线a,b被直线c所截.
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
(2)同旁内角∠1与∠3满足什么条件时,能得出a∥b?
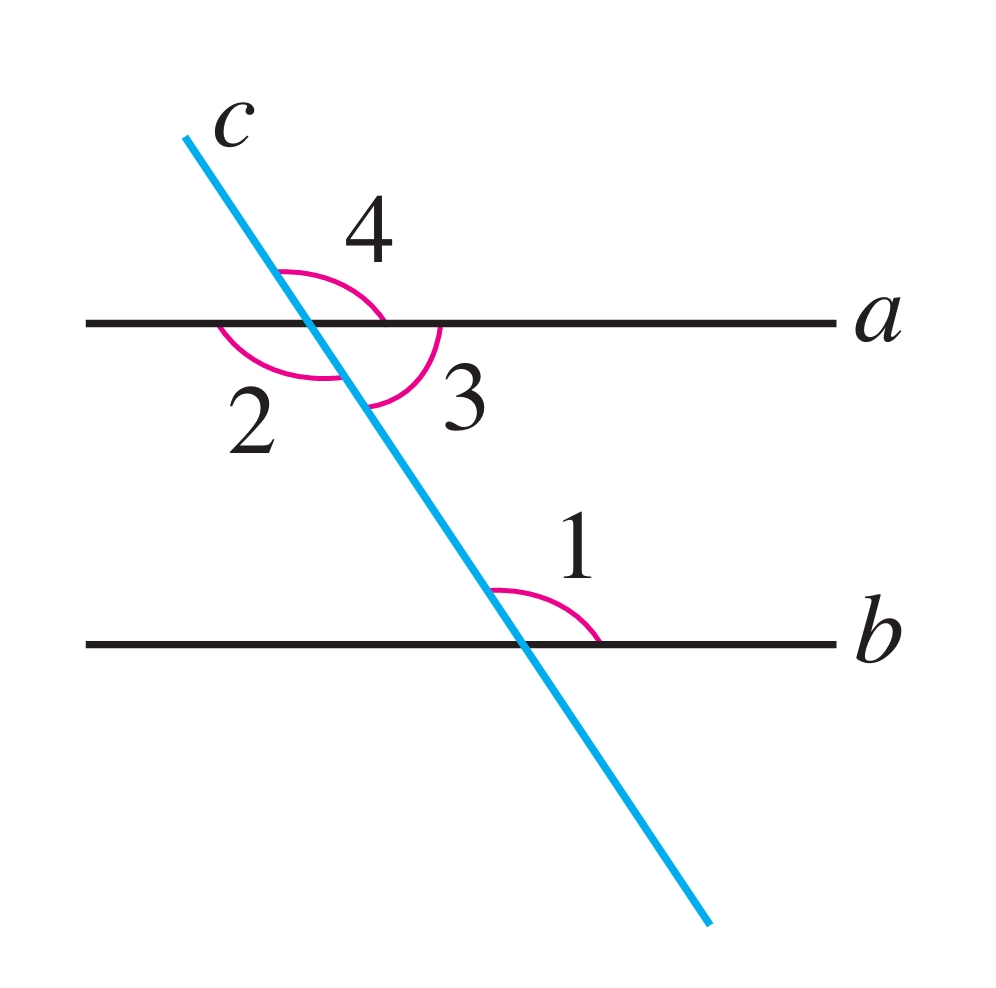
图7.2-7
如果∠1=∠2,由判定方法1,能得到a∥b,理由如下:因为∠1=∠2,而∠2=∠4(为什么?),所以∠1=∠4,即同位角相等,从而a∥b.
这样,就得到了利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
类似地,如果∠1与∠3互补,由判定方法1或判定方法2,能得到a∥b(为什么?). 这样,就得到了利用同旁内角判定两条直线平行的方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
例1
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
分析:
垂直总与直角联系在一起,进而可以用相应角的关系来判断两条直线是否平行.
解:
这两条直线平行. 理由如下:
图7.2-8
如图7.2-8,
∵ b⊥a,
∴ ∠1=90°.
同理 ∠2=90°.
∴ ∠1=∠2.
又 ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).
你还能利用其他方法说明b∥c吗?
练习
-
如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(1)如果∠B=∠DCG,那么可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,那么可以判断哪两条直线平行?为什么?
(3)如果∠D+∠DFE=180°,那么可以判断哪两条直线平行?为什么?
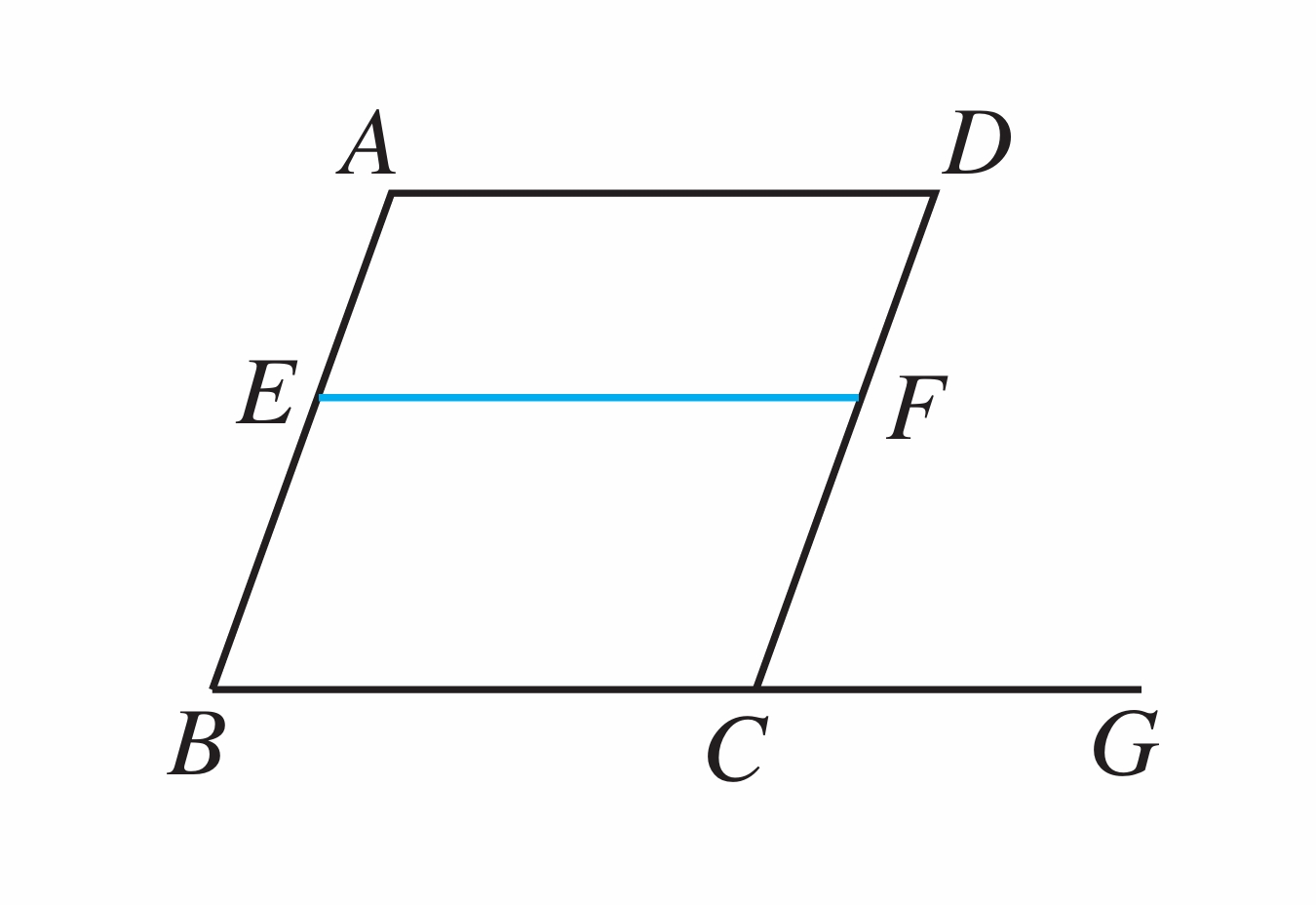
(第1题)
-
如图,木工常用角尺画平行线,你能说出其中的道理吗?
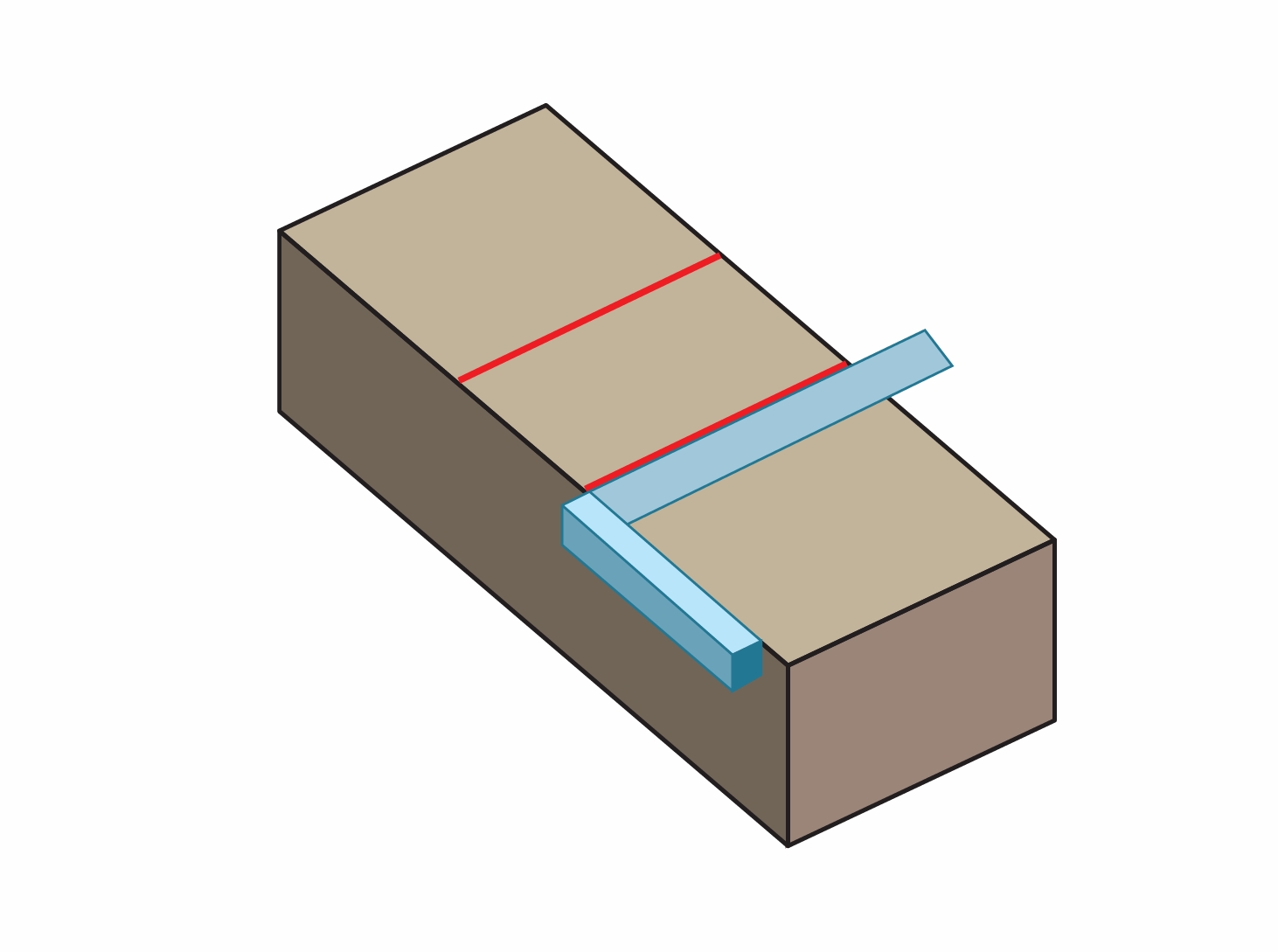
(第2题)
-
在铺设钢轨时,两条钢轨必须是互相平行的. 如图,已知∠2是直角,要判断两条钢轨是否平行,只需要再度量图中标出的哪个角?为什么?
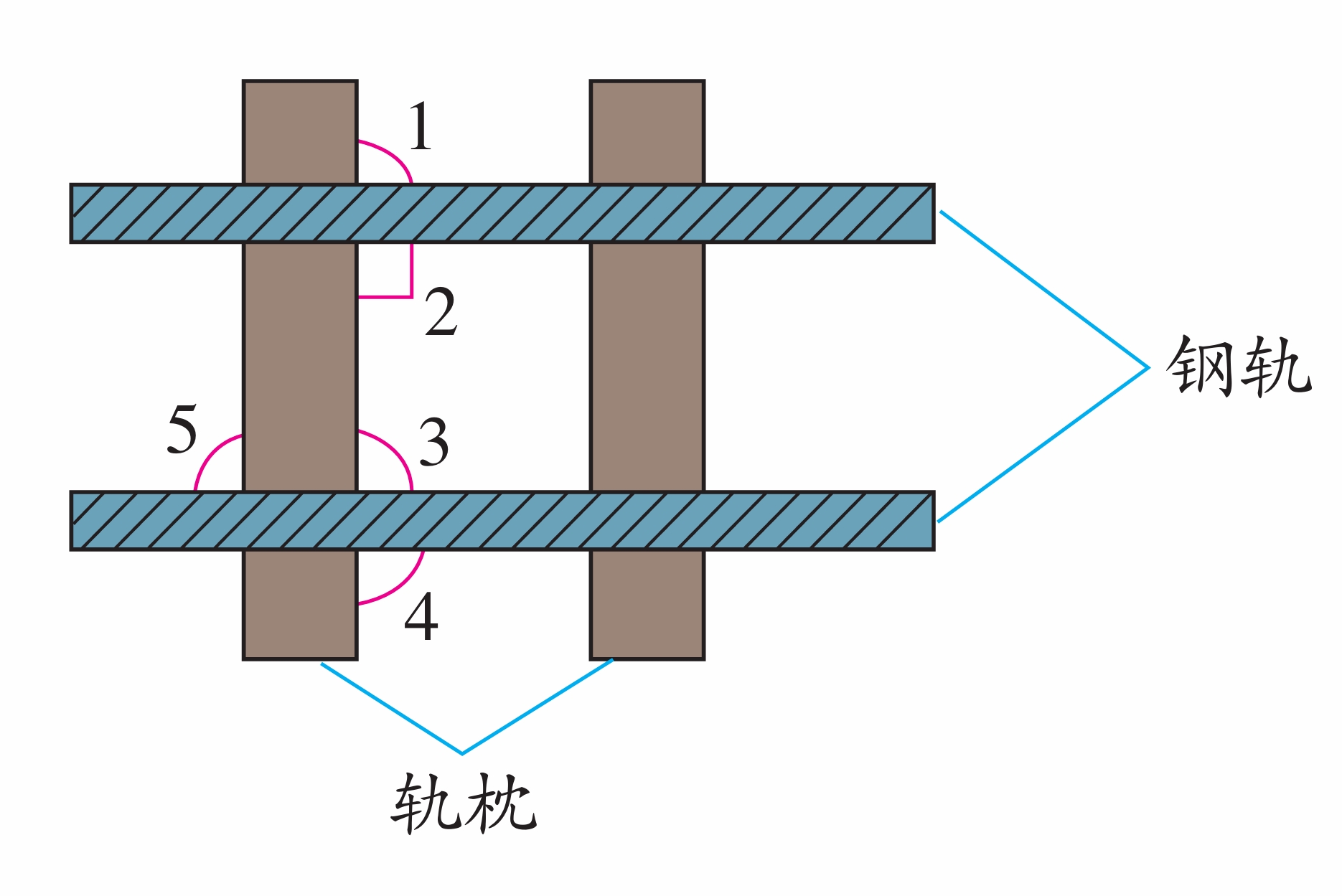
(第3题)
-
如图是两条道路互相垂直的交叉路口,你能画出它的平面示意图(用两条平行线段表示一条道路)吗?你能用类似的方法,画出两条道路成45°角的交叉路口的平面示意图吗?
(第4题)
本节小结
- 平行线的判定方法1:同位角相等,两直线平行
- 平行线的判定方法2:内错角相等,两直线平行
- 平行线的判定方法3:同旁内角互补,两直线平行
- 在同一平面内,垂直于同一条直线的两条直线互相平行
- 判定两条直线平行的关键是找到合适的角的关系(同位角、内错角或同旁内角)