7.2 平行线
除相交外,平行也是直线之间的基本位置关系.
本节我们将研究平行线。与相交线类似,我们借助两条直线被第三条直线所截形成的角,研究平行线的判定与性质.
7.2.1 平行线的概念
思考
如图7.2-1,将两根木条a,b分别与木条c钉在一起,并把它们想象成在同一平面内两端无限延伸的三条直线。固定木条b和c,转动木条a,直线a从在c的左侧与直线b相交逐步变为在c的右侧与直线b相交。想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
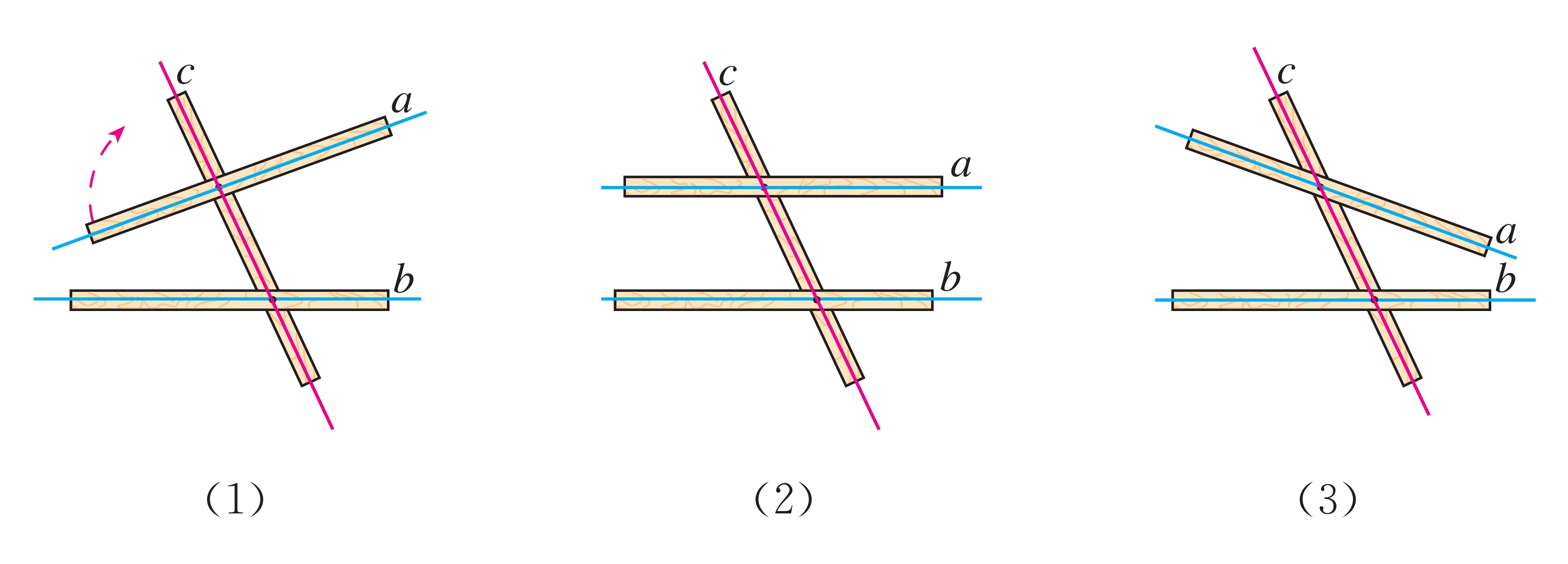
图7.2-1 转动木条a的过程中,直线a与b的位置关系
可以发现,在木条a转动的过程中,存在直线a与b不相交的位置。在同一平面内,当直线a,b不相交时,我们说直线a与b互相平行(parallel),记作"a∥b"。在同一平面内,不重合的两条直线只有两种位置关系:相交与平行。
在实际生活中,平行线随处可见,例如农田中平行的田垄、建筑物表面平行的栅格线(图7.2-2)。你还能举出其他例子吗?

图7.2-2 生活中的平行线例子
可以借助直尺和三角尺画平行线. 如图 7.2-3,保持直尺不动,沿直尺推动三角尺,分别画直线a,b,则a∥b.
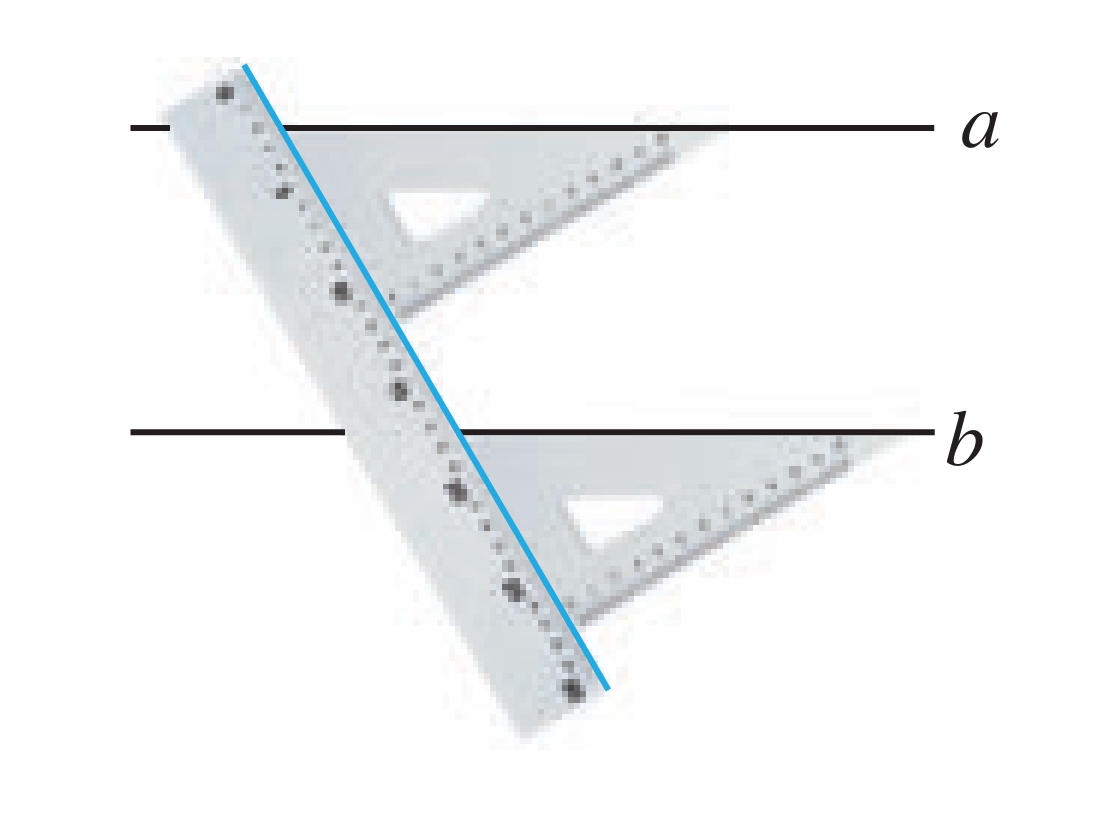
图7.2-3 用直尺和三角尺画平行线
思考
在图7.2-1转动木条a的过程中,有几个位置使得直线a与b平行?
如图7.2-4,过点B画直线a的平行线,能画出几条?过点C呢?
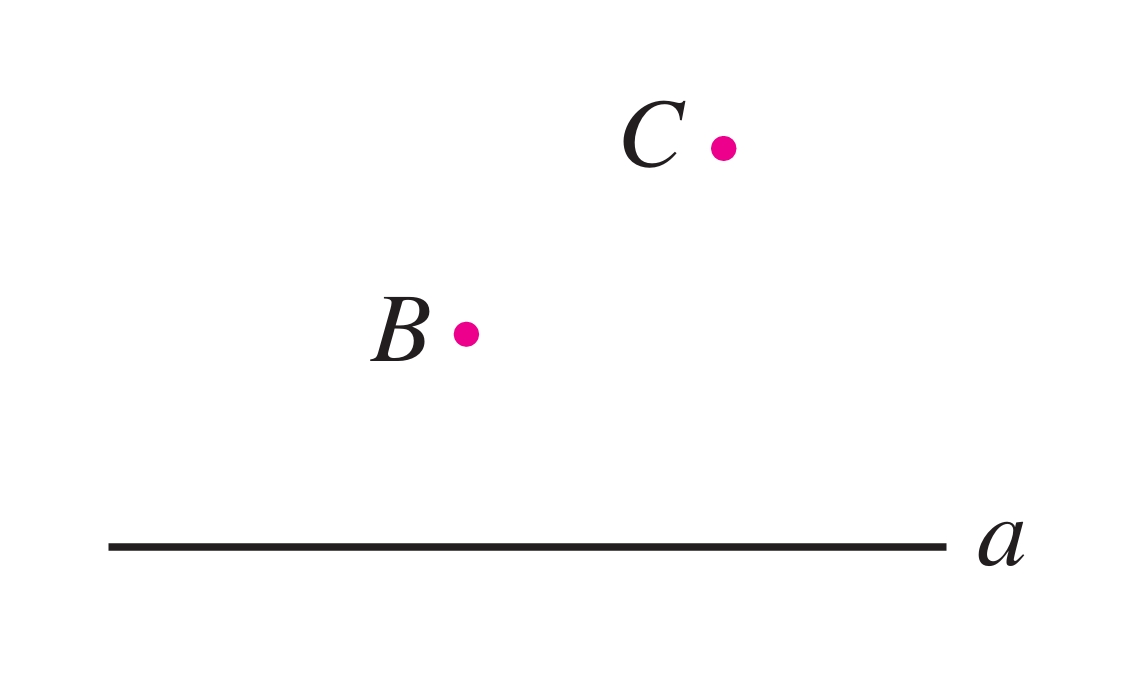
图7.2-4 过点画平行线
平行线的基本事实
一般地,有如下关于平行线的基本事实:
过直线外一点有且只有一条直线与这条直线平行。
由以上基本事实,可以进一步得到如下结论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
也就是说:如果b∥a,c∥a,那么b∥c(图7.2-5)。
图7.2-5 平行于同一条直线的两条直线互相平行
练习
如图,用直尺和三角尺画平行线:
-
过点A画MN∥BC;
-
过点C画CE∥DA,与AB交于点E;过点C画CF∥DB,与AB的延长线交于点F。
本节小结
- 在同一平面内,不相交的两条直线叫做平行线,记作"a∥b"。
- 在同一平面内,不重合的两条直线只有两种位置关系:相交与平行。
- 可以用直尺和三角尺画平行线。
- 平行线的基本事实:过直线外一点有且只有一条直线与这条直线平行。
- 平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。