7.1.4 观察与猜想
数学知识的演绎过程
在数学的学习过程中,我们常常经历这样的演绎过程:
- 观察:通过视觉、触觉等感官感知数学对象的表面特征
- 猜想:基于观察结果提出初步的假设或结论
- 验证:运用数学工具和方法(如度量、计算、逻辑推理)检验猜想的正确性
- 结论:根据验证结果得出最终的数学结论
然而,我们的观察有时会受到各种因素的影响,产生视觉或认知上的错觉,这就需要我们通过严谨的数学方法进行验证,确保结论的正确性。
观察与猜想:看图时的错觉
观察是数学研究的起点,通过观察我们可以发现规律、提出猜想。但观察也可能产生错觉,需要我们通过严谨的方法进行验证。
1. 线段长度的观察
观察图1每组中的线段 a 与 b 哪一条长?
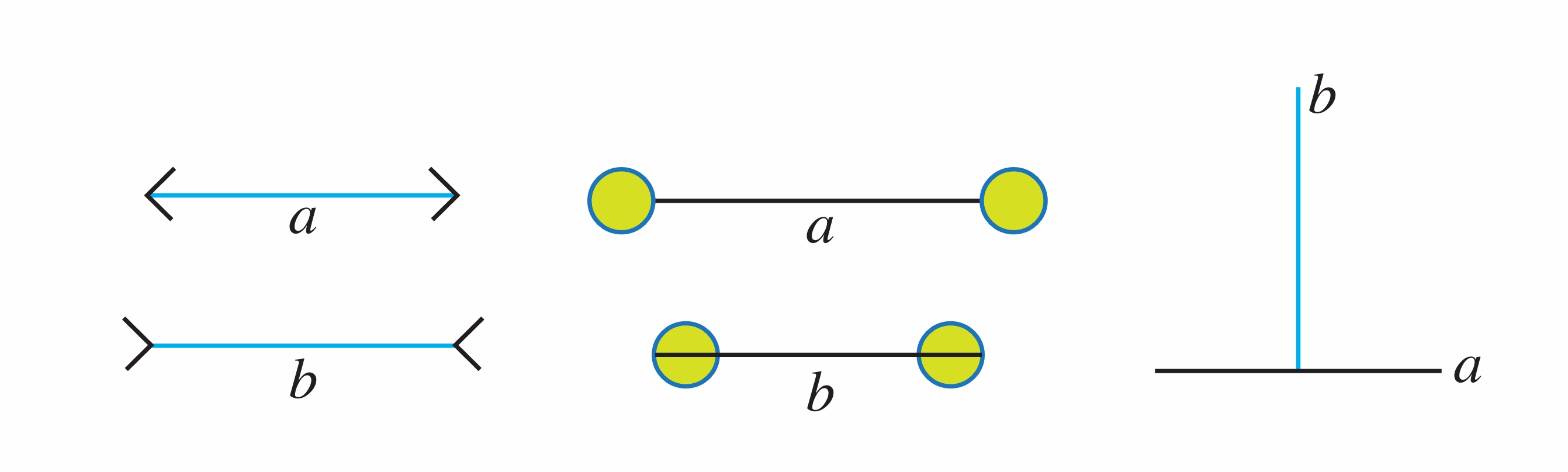
图1 线段长度的观察
数学演绎过程:
- 观察:通过视觉观察,可能会认为某些组中的线段 a 与 b 长度不同
- 猜想:基于观察,提出线段 a 与 b 长度可能不同的猜想
- 验证:使用刻度尺测量每组中线段 a 与 b 的实际长度
- 结论:通过测量发现,每组中的线段 a 与 b 长度相等,视觉差异是由线段周围的辅助元素(如箭头、圆点)引起的错觉
2. 圆大小的观察
观察图2每组中蓝色的圆 A 和圆 B 哪一个大?
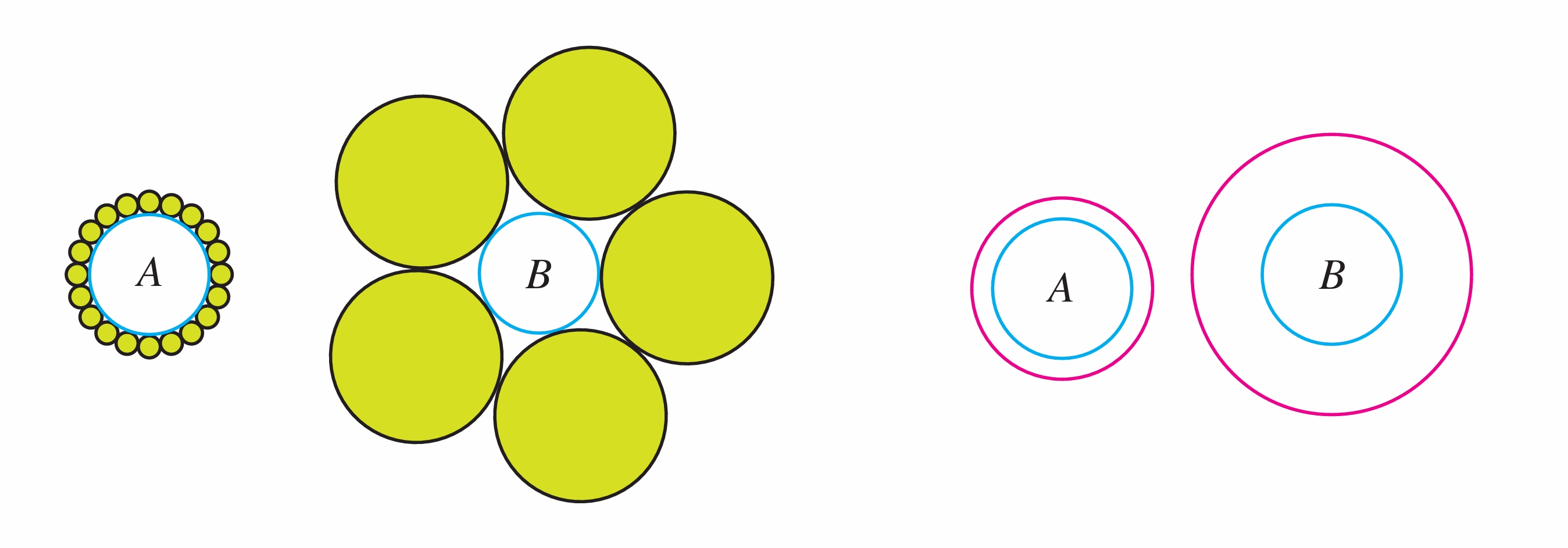
图2 圆大小的观察
数学演绎过程:
- 观察:通过视觉观察,可能会认为圆 A 比圆 B 大,因为圆 A 周围是小圆,而圆 B 周围是大圆
- 猜想:基于观察,提出圆 A 可能比圆 B 大的猜想
- 验证:使用圆规或刻度尺测量两个圆的直径或半径
- 结论:通过测量发现,圆 A 和圆 B 的直径/半径相等,视觉差异是由周围圆的大小对比引起的错觉
3. 平行线的观察
观察图3每组中蓝色的线段是否互相平行?如何检验?
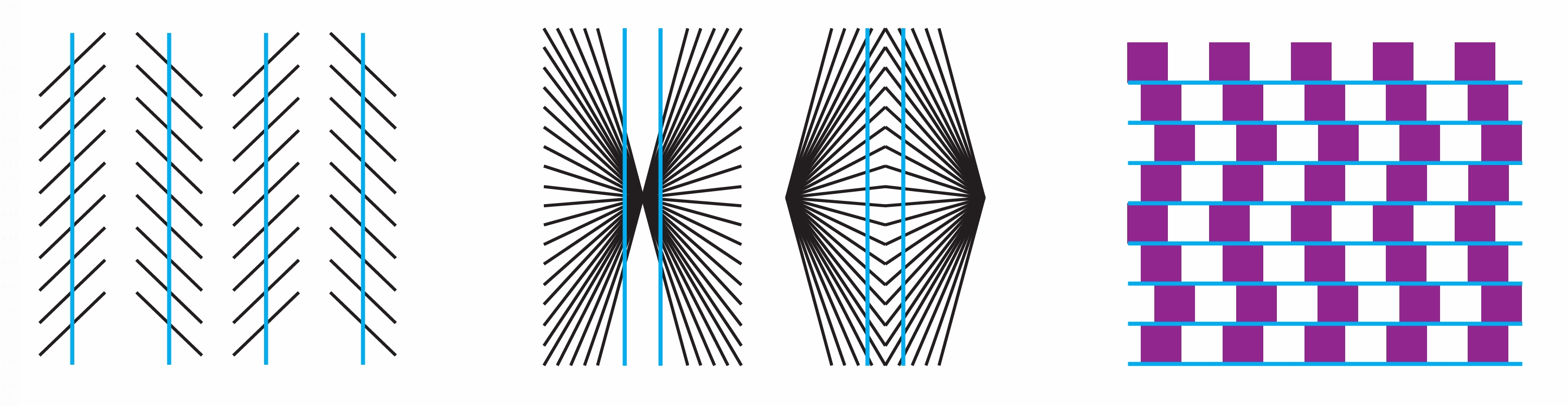
图3 平行线的观察
数学演绎过程:
- 观察:通过视觉观察,可能会认为蓝色线段不平行,因为背景线条的干扰
- 猜想:基于观察,提出蓝色线段可能不平行的猜想
- 验证:
- 使用直尺和三角板推平行线的方法检验
- 通过绘制截线,测量同位角或内错角是否相等
- 学习了平行线的判定定理后,可使用更严谨的方法验证
- 结论:通过验证发现,每组中的蓝色线段实际上是互相平行的,视觉差异是由背景线条的干扰引起的错觉
总结与反思
通过以上观察与猜想的活动,我们可以得出以下结论:
- 观察的局限性:人类的视觉感知可能会受到周围环境的影响,产生错觉,因此观察结果不能直接作为数学结论
- 验证的重要性:数学结论需要通过严谨的方法进行验证,如度量、计算、逻辑推理等
- 数学的严谨性:数学是一门严谨的学科,结论的得出必须基于严格的证明和验证
- 知识的应用:随着我们学习的深入(如平行线的判定定理),我们验证猜想的方法会更加科学和高效
在今后的数学学习中,我们应该始终保持"观察-猜想-验证-结论"的科学态度,培养严谨的数学思维习惯,确保我们的结论正确可靠。
本节小结
- 观察是数学研究的起点,但观察可能产生错觉
- 数学结论需要通过严谨的方法进行验证,如度量、计算、逻辑推理等
- 视觉错觉的存在提醒我们,在数学学习中要保持严谨的态度
- 随着知识的积累,我们验证猜想的方法会更加科学和高效
- "观察-猜想-验证-结论"是数学研究的基本方法,也是我们学习数学的重要思维模式