7.1.3 两条直线被第三条直线所截
课前导入
在前面的学习中,我们研究了两条直线相交的情形,认识了对顶角和邻补角的概念及性质。
现在,让我们从数学演绎推理的角度思考:如果在同一平面内,一条直线与两条直线分别相交,会形成怎样的几何图形?这些角之间又会存在怎样的位置关系呢?
首先,我们知道两条直线相交形成四个角,这些角之间存在对顶角相等、邻补角互补的关系。
接下来,我们进一步推广:当一条直线与两条直线相交时,会形成八个角。这些角中,除了有公共顶点的角(对顶角、邻补角)外,还有许多没有公共顶点的角。
那么,这些没有公共顶点的角之间,是否存在某种规律性的位置关系呢?这就是我们今天要研究的内容——两条直线被第三条直线所截形成的角的位置关系。
前面我们研究了一条直线与另一条直线相交的情形,接下来,我们进一步研究同一平面内一条直线与两条直线分别相交的情形。
图7.1-12 GeoGebra交互式数学画板
GeoGebra使用指南
- 点击工具栏中的直线工具绘制直线
- 使用移动工具拖动直线改变位置
- 使用角度工具测量角度
- 点击"文件"菜单保存或导出图形
- 可以通过工具栏切换不同的绘图工具
如图7.1-12,直线AB,CD与EF相交(也可以说两条直线AB,CD被第三条直线EF所截),构成八个角。我们已经学习了有公共顶点的角的关系,下面我们看那些没有公共顶点的两个角的关系。
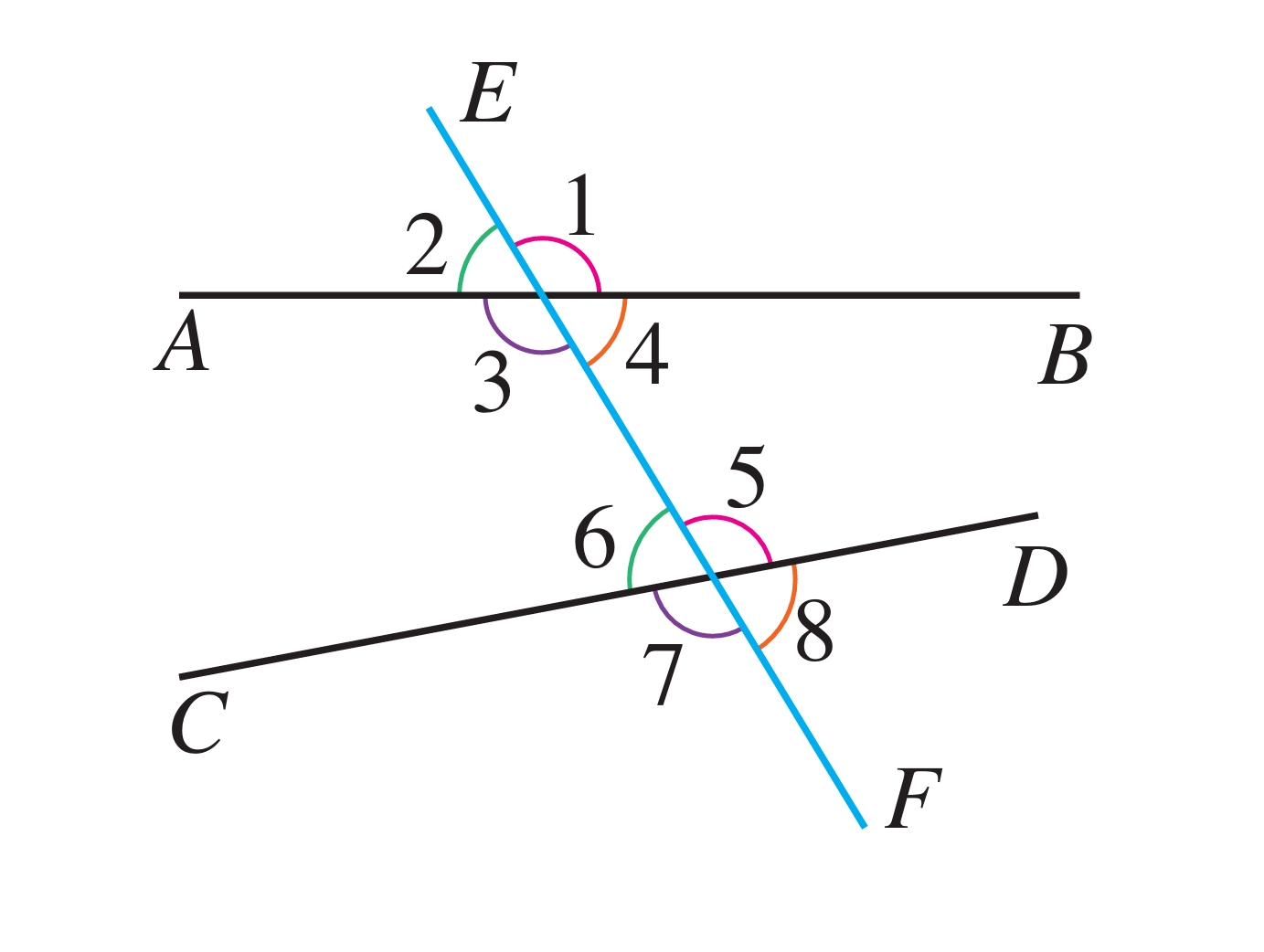
先看图7.1-12中的∠1和∠5,这两个角分别在直线AB,CD的同一侧(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫作同位角。
思考:∠2和∠6是同位角吗?图7.1-12中还有没有其他同位角?若有,标记出它们。
再看∠3和∠5,这两个角都在直线AB,CD之间,并且分别在直线EF的两侧(∠3在直线EF的左侧,∠5在直线EF的右侧),具有这种位置关系的一对角叫作内错角。∠3和∠6虽然也都在直线AB,CD之间,但是它们在直线EF的同一旁(左侧),具有这种位置关系的一对角叫作同旁内角。
思考:图7.1-12中还有没有其他内错角与同旁内角?若有,标记出它们。
图7.1-12 GeoGebra交互式数学画板
例3
如图7.1-13,直线DE,BC被直线AB所截。
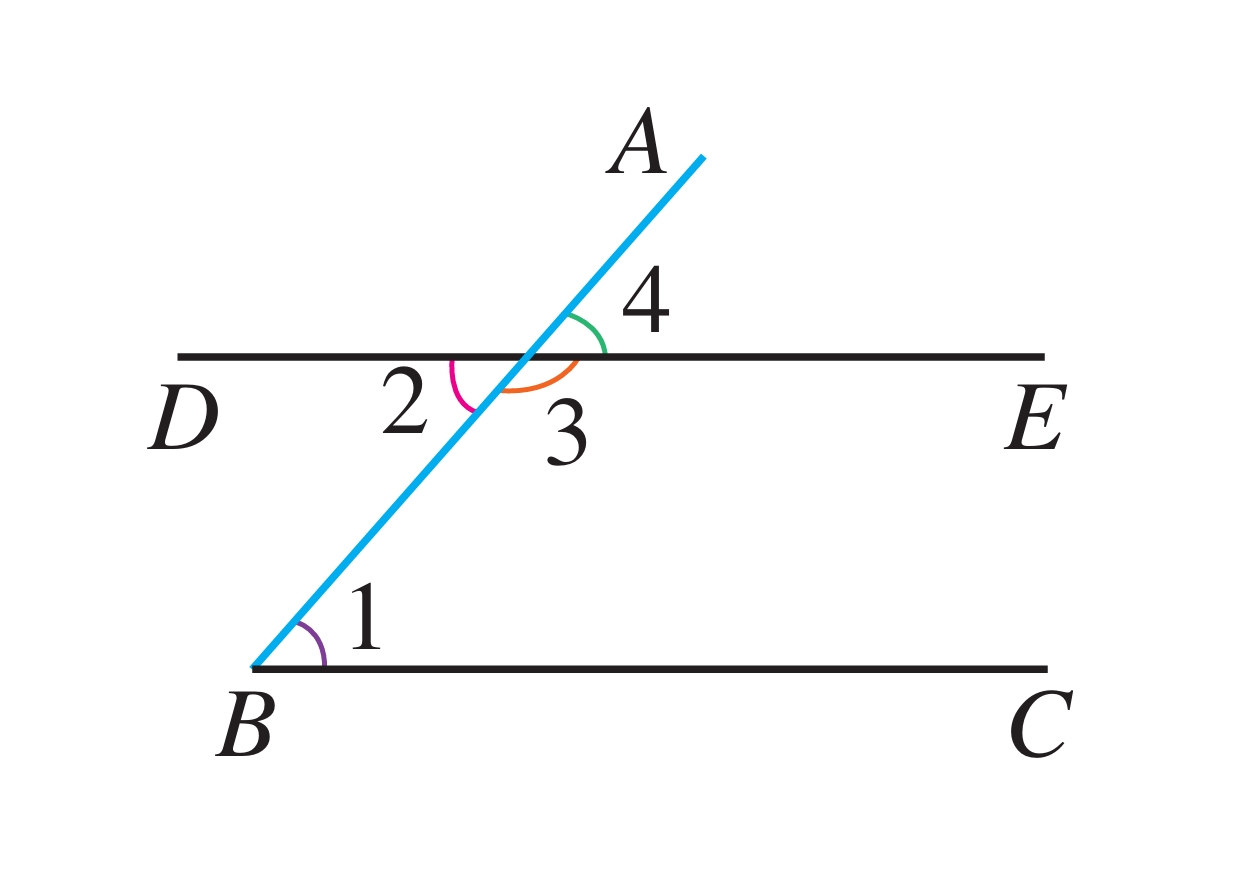
(1) ∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
解:
(1) ∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角。
(2) 如果∠1=∠4,又对顶角相等,可得∠2=∠4,因此∠1=∠2。
因为∠4和∠3互补,所以∠4+∠3=180°。又因为∠1=∠4,所以∠1+∠3=180°,即∠1和∠3互补。
练习
1. 分别指出下列各图中的同位角、内错角、同旁内角。
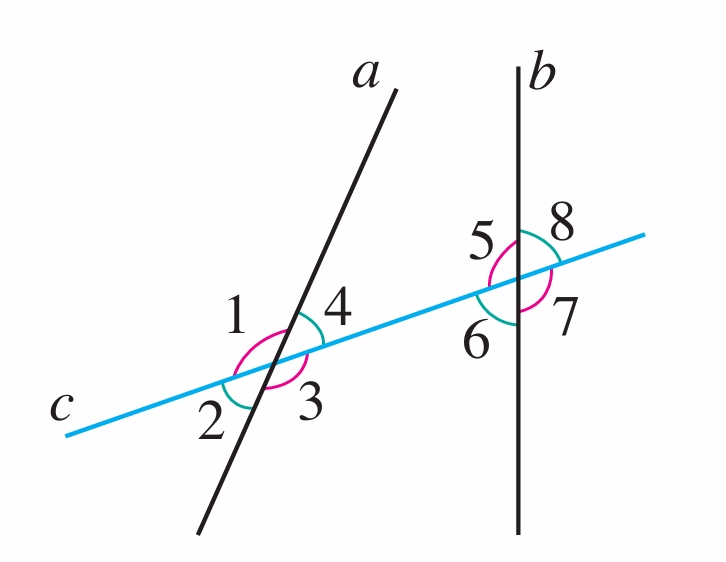
(1)
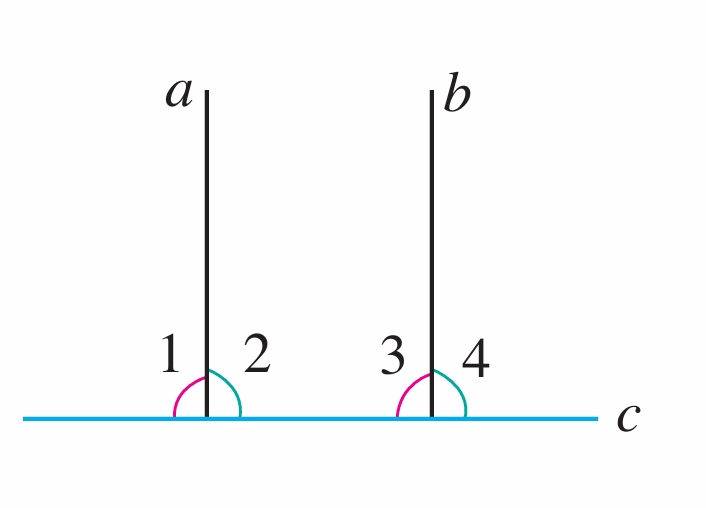
(2)
2. 如图,∠B与哪个角是内错角?与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论。
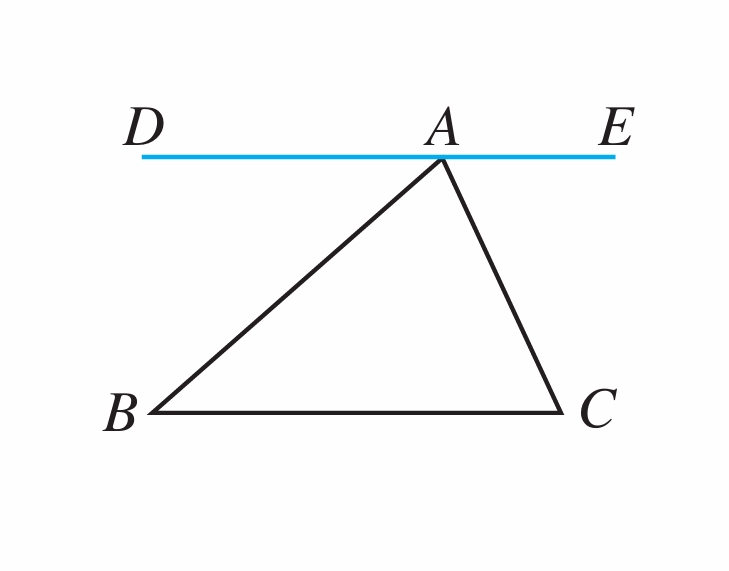
(第2题)
思维发散
3. 如图,AB⊥l,CB⊥l,B为垂足,那么A,B,C三点在同一条直线上吗?请说明理由。
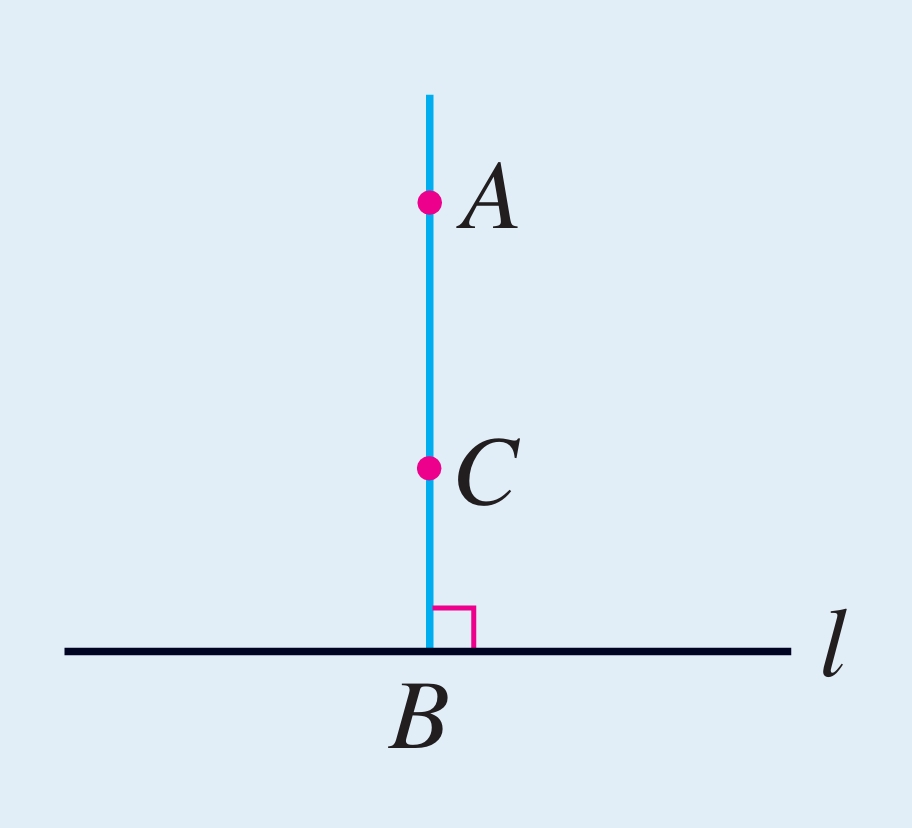
(第3题)
4. 直线AB,CD相交于点O。
(1) OE,OF分别是∠AOC,∠BOD的平分线。画出这个图形。
(2) 射线OE,OF在同一条直线上吗?为什么?
图7.1-13 GeoGebra交互式数学画板
本节小结
- 两条直线被第三条直线所截,形成八个角。
- 同位角:在两条被截直线的同一侧,且在截线的同侧的一对角。
- 内错角:在两条被截直线之间,且在截线的两侧的一对角。
- 同旁内角:在两条被截直线之间,且在截线的同一旁的一对角。
- 同位角、内错角、同旁内角是描述角的位置关系的重要概念,是后续学习平行线判定和性质的基础。