7.1.2 两条直线垂直
垂直是相交的一种特殊情形. 在相交线的模型(图 7.1-1)中,固定木条 a,转动木条 b. 当 b 的位置变化时,a,b 所成的∠α 也会发生变化. 当∠α=90°时(图 7.1-4),这两根木条垂直.
拖动木条可旋转,观察角度变化
∠aob = 45°
图7.1-4 相交线的木条模型
一般地,当两条直线 a,b 相交所成的四个角中,有一个角是直角时,我们说 a 与 b 互相垂直(perpendicular),记作 "a⊥b".
两条直线互相垂直,其中的一条直线叫作另一条直线的垂线,它们的交点叫作垂足. 在图 7.1-5 中,AB⊥CD,垂足为 O.
图7.1-5
由上可知,如果两条直线相交所成的四个角中有一个角等于 90°,那么这两条直线互相垂直. 在图 7.1-5 中,如果直线 AB,CD 相交于点 O,∠AOD=90°,那么 AB⊥CD. 这个推理过程可以写成下面的形式:
因为 ∠AOD=90°,
所以 AB⊥CD.
思考
反过来,如果 AB⊥CD,那么 ∠AOD 是多少度?写出这个推理过程.
在日常生活中,两条直线互相垂直的情形很常见,例如图 7.1-6 中窗户上互相垂直的木条、网球拍上互相垂直的网线. 你能再举出其他例子吗?

图7.1-6
接下来我们研究互相垂直的两条直线的性质.
探究
如图 7.1-7,用三角尺或量角器画已知直线 l 的垂线.
(1)经过直线l上一点 A 画 l 的垂线,这样的垂线能画出几条?
(2)经过直线 l 外一点 B 画 l 的垂线,这样的垂线能画出几条?
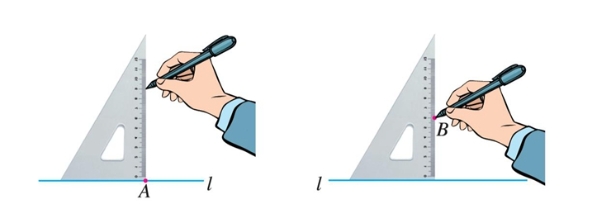
图7.1-7
拖动三角板可移动,按住旋转点可旋转,沿边缘绘制垂线
图7.1-7 交互式三角板工具
可以发现,经过一点(在已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线. 由此得到关于垂线的基本事实:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
例2 如图7.1-8,过点P画出射线AB或线段AB的垂线.
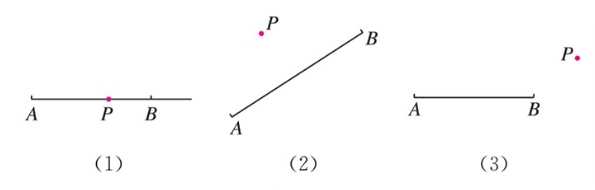
图7.1-8
画一条射线或线段的垂线,就是画它们所在直线的垂线.
解:如图7.1-9所示.
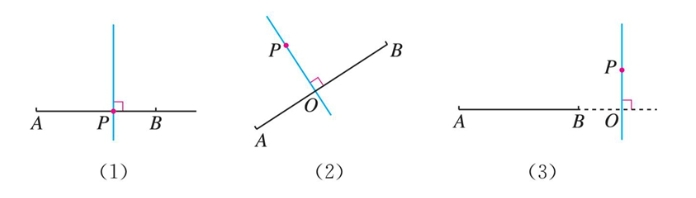
图7.1-9
我们再来研究互相垂直的两条直线的另一个性质.
思考
如图 7.1-10,在灌溉时,要把河中的水引到农田 P 处,如何挖渠能使渠道最短?

图7.1-10
探究
如图 7.1-11,P 是直线 l 外一点,PO⊥l,垂足为 O,我们称 PO 为点 P 到直线 l 的垂线段。A 是直线 l 上除点 O 外一点,连接 PA。测量并比较线段 PO 与 PA 的长度,你能得到什么结论?改变点 A 的位置呢?
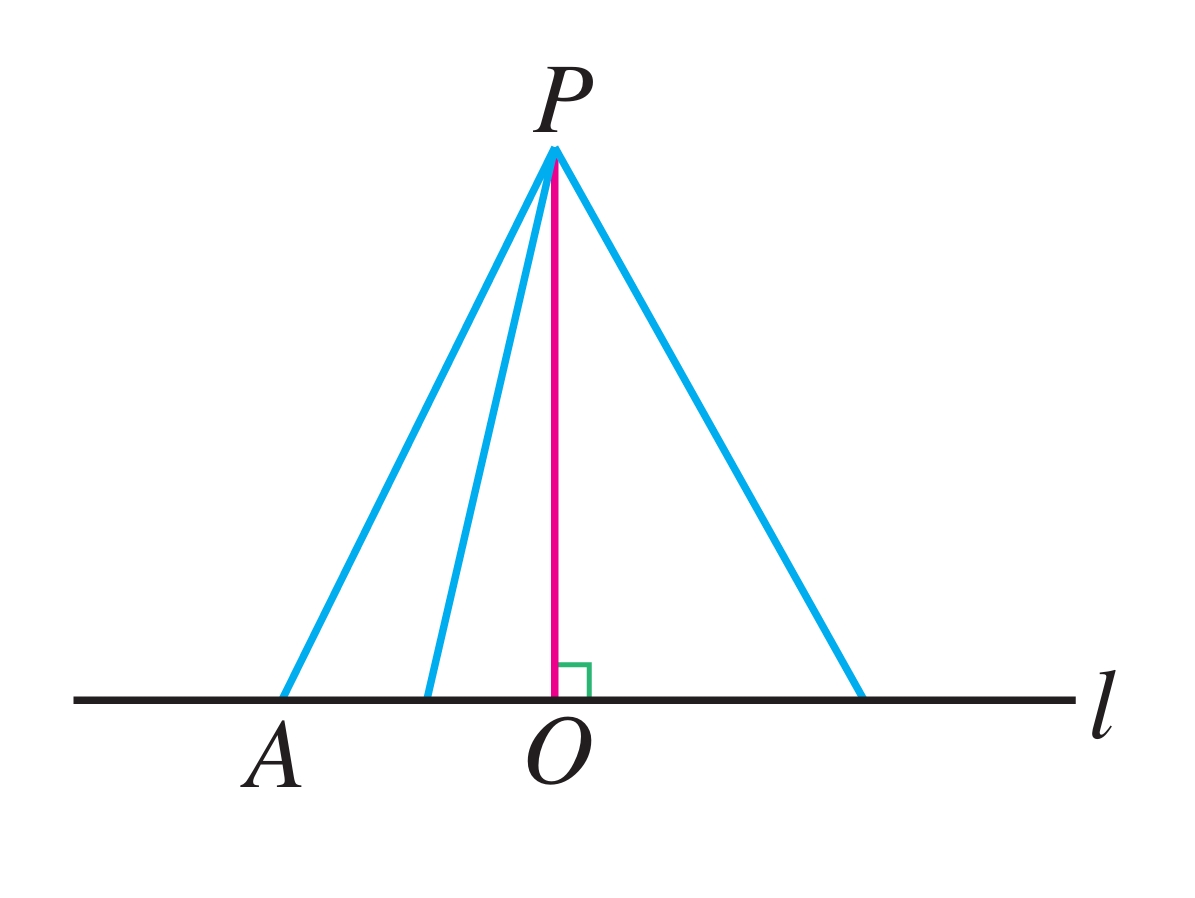
图7.1-11
你也可以利用信息技术工具,在直线 l 上拖动点 A,改变点 A 的位置,探究 PO 与 PA 的长度关系。
拖动点 A 改变位置,观察 PO 与 PA 的长度关系
PO = 4.7 cm
PA = 5.8 cm
图7.1-11 交互式探究
可以发现,连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
对于图 7.1-10,现在你知道如何挖渠能使渠道最短了吗?
练习
1. 当两条直线相交所成的四个角都相等时,这两条直线有什么位置关系?为什么?
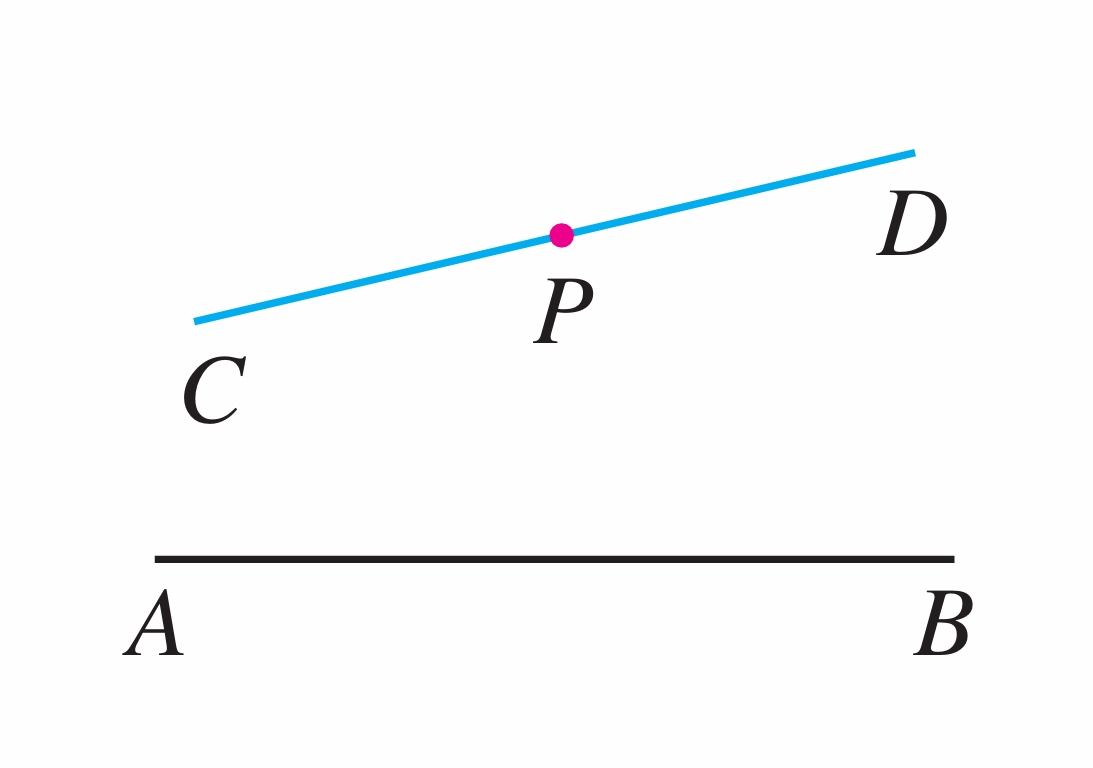
2. 如图,分别过点 P 画直线 AB,CD 的垂线,并量出点 P 到直线 AB 的距离。
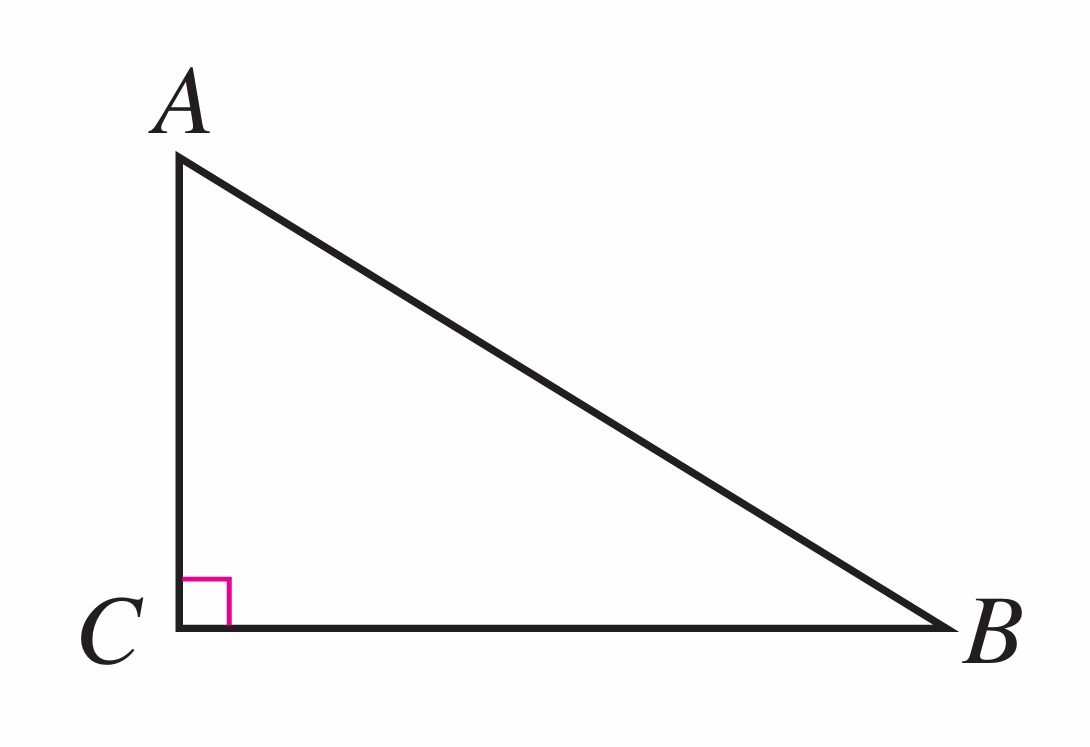
3. 如图,在三角形 ABC 中,∠C=90°。
(1) 分别指出点 A 到直线 CB,点 B 到直线 AC 的距离是哪些线段的长度;
(2) 三条边 AB,AC,CB 中哪条边最长?为什么?
本节小结
- 两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
- 过一点有且只有一条直线与已知直线垂直。
- 连接直线外一点与直线上各点的所有线段中,垂线段最短。
- 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
- 利用三角板可以过一点画已知直线的垂线,操作时要确保三角板的直角边与已知直线重合。