7.1.1 两条直线相交
在上一章中,我们认识了相交线,知道相交是直线之间的一种基本位置关系。
图7.1
图7.1中,a是一条直线,a直线将平面分成了两个区域,我们把这两个区域叫做a直线的两部分
图7.2
图7.2中,a,b是两条直线,它们相交于一点,a、b两直线把平面分成了四个区域。
我们可以用角的位置关系和数量关系来刻画相交线的位置关系。
7.1.1 两条直线相交
如图7.1-1,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型。在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
拖动木条可旋转,观察角度变化
∠aob = 45°
图7.1-1 相交线的木条模型
探究
任意画两条相交的直线,形成四个角(图7.1-2),∠1和∠2有怎样的位置关系?∠1和∠3呢?
分别量一量各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
利用下方信息技术工具,改变两条直线相交所成的角的大小,上述关系还保持吗?为什么?
拖动直线可旋转,观察四个角的关系
图7.1-2 相交直线形成的角
∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种位置关系的两个角,互为邻补角。
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
思考:
图7.1-2中还有没有其他邻补角与对顶角?
在图7.1-2中,∠1=∠3。这个结论还可以通过补角的性质得到:∠1与∠2互补,∠3与∠2互补,由“同角的补角相等”,可得∠1=∠3。类似地,可得∠2=∠4。这样,可以得到对顶角的性质:
对顶角相等。
上面推出“对顶角相等”这个结论的过程,可以写成下面的形式:
因为 ∠1与∠2互补,∠3与∠2互补,
所以 ∠1=∠3(同角的补角相等)。
例1
如图7.1-3,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数。
图7.1-3
解:
由∠1和∠2互为邻补角,得
∠2=180°-∠1=180°-40°=140°。
由对顶角相等,得
∠3=∠1=40°,∠4=∠2=140°。
互动练习
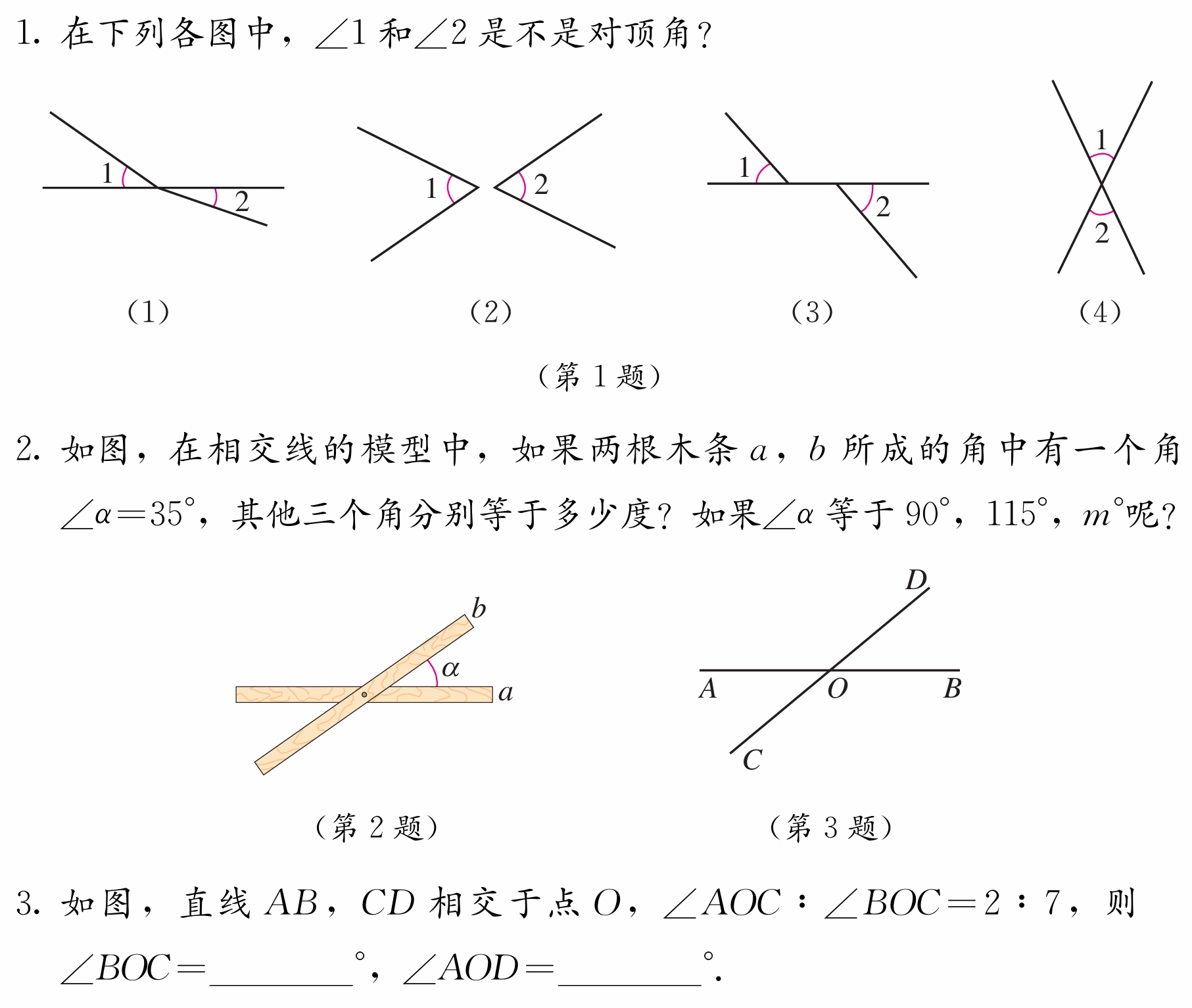
小结
- 邻补角:有一条公共边,另一边互为反向延长线的两个角
- 对顶角:有一个公共顶点,两边分别互为反向延长线的两个角
- 对顶角的性质:对顶角相等
- 邻补角的性质:邻补角互补